問題來源：
假設小王所在公司每月10日發(fā)工資,，現在為2020年6月10日,，要求完成下列計算：
（1）小王2020年6月10日將10000元現金存入銀行,，若年利率為12%,，每年復利一次,，2025年6月10日小王可從銀行取出多少錢？
復利終值F=10000×（F/P,，12%,，5）=10000×1.7623=17623（元）
（2）若年利率為12%，每年復利一次,，小王希望2030年6月10日能夠取出10000元,，則其現在應存入銀行多少錢？
復利現值P=10000×（P/F,，12%,，10）=10000×0.3220=3220（元）
（3）若年利率為12%，每半年復利一次，小王希望2030年6月10日能夠取出10000元,，則其現在應存入銀行多少錢,？
復利現值P=10000×（P/F，6%,，20）=10000×0.3118=3118（元）
（4）若要使4年后的復利終值變?yōu)楸窘鸬?倍,，每半年復利一次，則其實際年利率應為多少,？
設本金為P,，半年利率為i
則，3P=P×（F/P,，i,，8）
（F/P，i,，8）=3
因為：（F/P,，14%，8）=2.8526,，（F/P,，15%，8）=3.0590
所以,，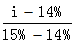
=
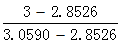
i=14.71%
實際年利率=（1+14.71%）2-1=31.58%
（5）2020年6月10日購買一部手機,，有兩種付款方式，一是：首付1000元,，以后每月10日分期付款500元,，連續(xù)付10次；二是：在2020年6月10日一次付清,。若月利率為1%,，小王選擇方案二即一次付清，付款額為多少才合算,。（★★）
付款額低于5735.65元才合算,。
樊老師
2020-07-18 08:57:33 5533人瀏覽
這里說的是一次付清，也就是計算的是現值,，而不是終值,，是使方案二現在一次支付的款項等于方案一的現值。方案一中是首付1000元,，也就是0時點支付1000元,，所以不需要進行折現,，以后每月10日分期付款500元，符合年金的形式,，所以需要乘以年金現值系數折現到0時點,。
您再理解一下，如有其他疑問歡迎繼續(xù)交流,，加油,！相關答疑
-
2024-08-09
-
2024-07-07
-
2024-06-16
-
2023-11-24
-
2022-04-29
您可能感興趣的中級會計試題
津公網安備12010202000755號