問(wèn)題來(lái)源:
![]() DL公司2022年12月10日欲購(gòu)置一批電腦,,銷(xiāo)售方提出三種付款方案,,具體如下:
DL公司2022年12月10日欲購(gòu)置一批電腦,,銷(xiāo)售方提出三種付款方案,,具體如下:
方案1:2022年12月10日付款10萬(wàn)元,從2024年開(kāi)始,,每年12月10日付款28萬(wàn)元,,連續(xù)支付5次。
方案2:2022年12月10日付款5萬(wàn)元,,從2023年開(kāi)始,,每年12月10日付款25萬(wàn)元,連續(xù)支付6次,。
方案3:2022年12月10日付款10萬(wàn)元,,從2023年開(kāi)始,6月10日和12月10日付款,,每次支付15萬(wàn)元,,連續(xù)支付8次,。
假設(shè)DL公司計(jì)算時(shí)間價(jià)值使用的年利率為10% ,,DL公司應(yīng)該選擇哪個(gè)方案,?
|
【答案】方案1的付款現(xiàn)值=10+28×(P/A,10%,,5)×(P/F,,10%,1)=10+28×3.7908×0.9091=106.49(萬(wàn)元),。
【解析】方案2:2019年12月10日付款5萬(wàn)元,,從2020年開(kāi)始,每年12月10日付款25萬(wàn)元,,連續(xù)支付6次,。把2019年12月10日作為0時(shí)點(diǎn),方案2的付款形式如下圖所示,。
方案2的付款現(xiàn)值=5+25×(P/A,,10%,6)=5+25×4.3553=113.88(萬(wàn)元) 【解析】方案3:2019年12月10日付款10萬(wàn)元,,從2020年開(kāi)始,,6月10日和12月10日付款,每次支付15萬(wàn)元,,連續(xù)支付8次,。 把2019年12月10日作為0時(shí)點(diǎn),方案3的付款形式如下圖所示,。
方案3中,,等額付款間隔時(shí)間為半年,折現(xiàn)率為10%/2=5%,。 方案3的付款現(xiàn)值=10+15×(P/A,,5%,8)=10+15×6.4632=106.95(萬(wàn)元) 由于方案1的付款現(xiàn)值最小,,所以應(yīng)該選擇方案1,。 |

楊老師
2022-04-13 12:42:02 2087人瀏覽
如果計(jì)算終值,,這是比較麻煩的,,需要把三個(gè)方案統(tǒng)一到一個(gè)終值點(diǎn)上。
方案1:2022年12月10日付款10萬(wàn)元,,從2024年開(kāi)始,,每年12月10日付款28萬(wàn)元,連續(xù)支付5次,。
方案2:2022年12月10日付款5萬(wàn)元,,從2023年開(kāi)始,,每年12月10日付款25萬(wàn)元,連續(xù)支付6次,。
方案3:2022年12月10日付款10萬(wàn)元,,從2023年開(kāi)始,6月10日和12月10日付款,,每次支付15萬(wàn)元,,連續(xù)支付8次。
方案一的終值點(diǎn)在2028年12月10,,方案二的終值點(diǎn)在2028年12月10日,,方案三的終值點(diǎn)2026年12月10日
這樣方案一的終值=10*(F/P,10%,,6)+28*(F/A,,10%,5)
方案二的終值=5*(F/P,10%,6)+25*(F/A,10%,,6)
方案3的終值=10*(F/A,,5%,12)+15*(F/A,,5%,,8)*(F/P,5%,,4)
相關(guān)答疑
-
2025-07-01
-
2025-06-28
-
2025-06-11
-
2025-06-09
-
2019-07-20
您可能感興趣的中級(jí)會(huì)計(jì)試題
中級(jí)會(huì)計(jì)相關(guān)知識(shí)專(zhuān)題





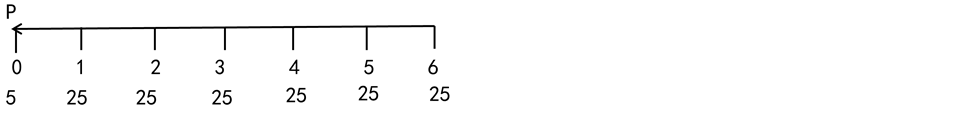




 津公網(wǎng)安備12010202000755號(hào)
津公網(wǎng)安備12010202000755號(hào)