問題來源：
“一零零”·掌握技巧必備技能：系數(shù)與列式
①終值vs現(xiàn)值——未來：終值；現(xiàn)在：現(xiàn)值
②復(fù)利vs年金—— 口訣：只有一次走復(fù)利，每年都有走年金
③列式技巧
復(fù)利終值F=P×（F/P,，i,，n）
復(fù)利現(xiàn)值P=F×（P/F，i,，n）
年金終值F=A×（F/A,，i，n）
年金現(xiàn)值P=A×（P/A,，i,，n）
等式兩邊有3個數(shù)據(jù)，系數(shù)需自行確定,，另外2個數(shù)據(jù)中,，一個已知，求解另一個即可,。
2.預(yù)付年金
預(yù)付年金,，每期期初收付的年金。
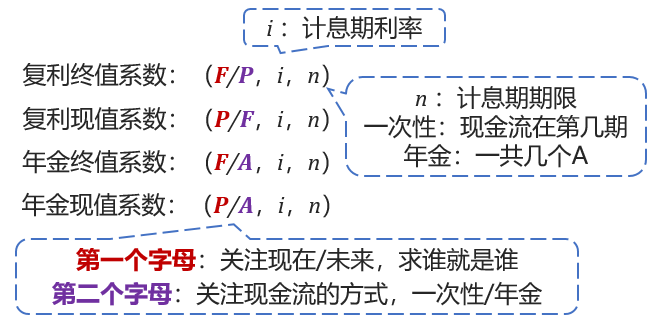
普通年金終值 | 預(yù)付年金終值 | |
方法一 |  | 相當于普通年金提早一期開始,，多生成一期利息,， 預(yù)付年金終值=普通年金終值（1+i） |
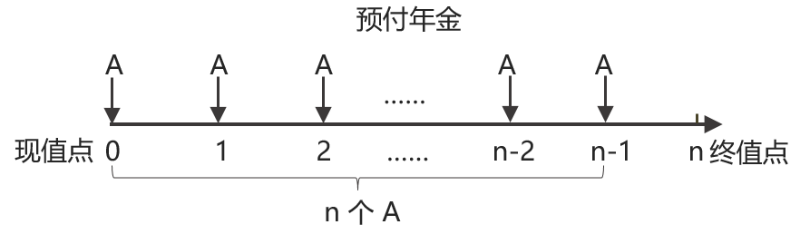
方法二 | 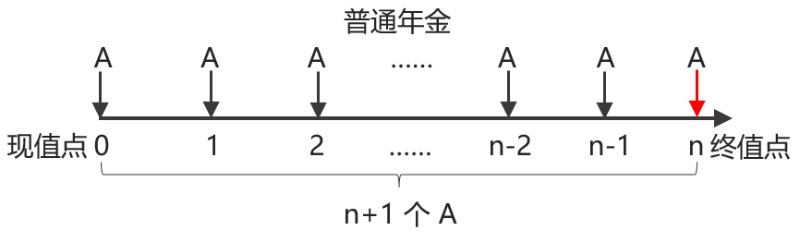 | 相當于n+1期的普通年金沒有在第n期存入本金，少了最后一期本金 預(yù)付年金終值=n+1期普通年金終值-A =A（F/A,，i,，n+1）-A =A[（F/A，i,，n+1）-1] 預(yù)付年金終值：期數(shù)+1,，系數(shù)-1 |
普通年金現(xiàn)值 | 預(yù)付年金現(xiàn)值 | |
方法一 | 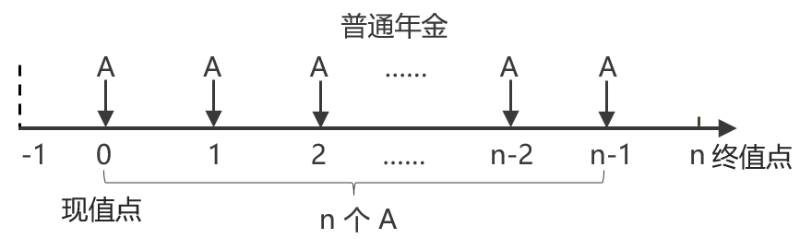 | 如果將-1時點作為現(xiàn)值點，預(yù)付年金相當于n期的普通年金,，從-1時點到0時點（真正的現(xiàn)值點）,，普通年金產(chǎn)生了一期利息 預(yù)付年金現(xiàn)值=普通年金現(xiàn)值（1+i） |
方法二 | 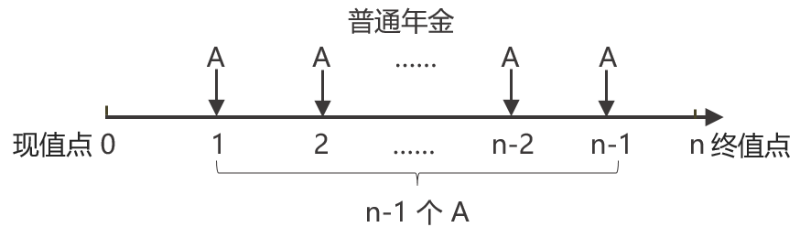 | 相當于n-1期的普通年金，在現(xiàn)值點又存入本金 預(yù)付年金現(xiàn)值=n-1期普通年金現(xiàn)值+A =A（P/A,，i,，n-1）+A =A[（P /A，i,，n-1）+1] 預(yù)付年金現(xiàn)值：期數(shù)-1,，系數(shù)+1 |
“一零零”·總結(jié)預(yù)付年金與普通年金的關(guān)系
方法 | 具體計算 | 記憶技巧 |
方法一 | 預(yù)付年金=普通年金×（1+i） 預(yù)付年金終值（現(xiàn)值）系數(shù) =普通年金終值（現(xiàn)值）系數(shù)×（1+i） | 先付款，更值錢 |
方法二 | 在普通年金系數(shù)的基礎(chǔ)上： 預(yù)付年金終值系數(shù)：期數(shù)+1,，系數(shù)-1 預(yù)付年金現(xiàn)值系數(shù)：期數(shù)-1,，系數(shù)+1 | 期終考試加分（期：期數(shù)，終：終值,，加：+1） 終值是期數(shù)+1，則系數(shù)-1 現(xiàn)值與終值剛好相反 |
查看完整問題
劉老師
2025-04-12 16:18:32 436人瀏覽
尊敬的學(xué)員，您好：
預(yù)付年金每期的現(xiàn)金流都比普通年金早一期支付,，相當于每筆錢都多賺了一期利息,。
比如同樣3年期：
普通年金：三期金額分別在1、2,、3年末存入,，利息積累2、1,、0期,；
預(yù)付年金：三期金額直接在0、1,、2年初存入,，利息積累3、2,、1期,。
相當于所有錢都比普通年金多“生長”了一次利息周期，因此終值整體要乘以（1+i）,。期數(shù)n看似相同,，但利息積累次數(shù)才是關(guān)鍵。
有幫助(1)
答案有問題,？
相關(guān)答疑
-
2025-07-01
-
2025-06-30
-
2025-06-10
-
2025-06-04
-
2023-09-02
您可能感興趣的中級會計試題
中級會計相關(guān)知識專題
津公網(wǎng)安備12010202000755號