遞延年金現(xiàn)值期數(shù)如何確定,？
這題（三）的計算里方法二里不明白為什么是m+n是9，不是10 ,，不是從第四年年末起,，連續(xù)6年嗎
問題來源：
第二部分 遞延年金
一、遞延年金終值
首個現(xiàn)金流發(fā)生在第2期或以后的年金,，叫做遞延年金,，一般用m表示遞延期數(shù)。
遞延年金終值和普通年金終值計算的方法一致,。
公式F=A×（F/A,，i，n）
其中,，每年收付金額為A,，利率為i，期數(shù)為n,，和遞延期數(shù)m無關,。
二、遞延年金現(xiàn)值
（一）方法一：先求遞延期末的現(xiàn)值,，再通過復利現(xiàn)值過程求0時點現(xiàn)值,。
公式：Pm=A×（P/A，i,，n）以及P0=Pm×（1+i）-m
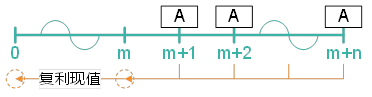
（二）方法二：假設1～m期也有現(xiàn)金流,，用m+n期年金的現(xiàn)值減去m期年金的現(xiàn)值。
公式：P0=Pm+n-Pm=A×（P/A,，i,，m+n）-A×（P/A，i,，m）
（三）計算
從第4年年末起,，連續(xù)6年每年存款4萬元，年利率5%,，該遞延年金的現(xiàn)值是多少,？
【方法一】查年金現(xiàn)值系數(shù)表可得（P/A，5%,，6）=5.0757
P3=A×（P/A,，5%，6）=4×5.0757=20.30（萬元）
P0=P3/（1+5%）3=17.54（萬元）,。
【方法二】查年金現(xiàn)值系數(shù)表可得
（P/A，5%,，9）=7.1078,，（P/A，5%,，3）=2.7232
P0=A×[（P/A,，5%,，9）-（P/A，5%,，3）]=4×（7.1078-2.7232）=17.54（萬元）,。
樊老師
2020-07-10 17:27:57 2977人瀏覽
這里說從第4年年末起,，也就是第4年年末就已經(jīng)開始付款了,，也就是時間軸上的4時點開始有現(xiàn)金流，所以遞延期是3期,；又因付款6期,，所以m+n是9。
每個努力學習的小天使都會有收獲的,，加油,！相關答疑
-
2024-07-18
-
2023-11-09
-
2022-08-12
-
2020-09-12
-
2020-08-27
津公網(wǎng)安備12010202000755號