問題來源：
練習18-計算分析題
要求：
（1）計算每張認股權證的價值
（2）計算該公司附認股權證債券的籌資成本。
（3）假設普通債券市場利率為9%,，分析該附認股權證的債券在財務上是否合理,？
（4）發(fā)行公司如何調整票面利率，投資者可以接受,？（票面利率調整必須以1個百分點為單位）
（5）發(fā)行公司如何調整認購價格,，投資者可以接受？（認購價格調整必須以1元為單位）
【答案】
（1）附權證債券的整體組合價格=1000（元）
純債券價值=1000×7%×(P/A,9%,20)+1000×(P/F,9%,20)=817.395（元）
每張認股權證的價值=（1000-817.395）/20=9.13（元）
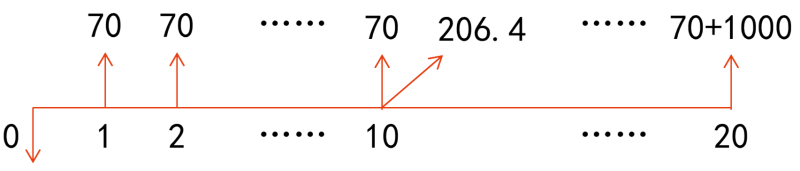
（2）購買1000元認股權證和債券組合的現(xiàn)金流量如下：
第1年初：流出現(xiàn)金1000元,，購買債券和認股權證
第1～20年：每年利息流入70元
第10年末：行權支出=19元/股×20股=380（元）
取得股票的市價=18元×（1+5%）10元/股×20股=29.32×20 =586.40（元）
現(xiàn)金凈流入=586.40-380=206.4（元）
第20年末：取得歸還本金1000元
根據(jù)上述現(xiàn)金流量計算出內含報酬率：
70×（P/A,，rd，20）+206.4×（P/F,，rd,，10）+1000×（P/F，rd,，20）=1000
估算收益率=（70+206.4/20）/1000=8.03%
試錯,，假設rd=8%，
70×（P/A，8%,，20）+206.4×（P/F,，8%，10）+1000×（P/F,，8%,，20）=997.37
調低折現(xiàn)率，假設rd=7%,，
70×（P/A,，7%，20）+206.4×（P/F,，7%,，10）+1000×（P/F，7%,，20）=1104.89
運用內插法：
（rd-7%）/（8%?7%）=（1000?1104.89）/（997.37?1104.89）,，解得：rd=7.98%
（3）不合理。
因為附認股權證債券的投資風險大于普通債券,，因此該附認股權證債券內含報酬率應比直接投資普通債券市場利率高,，但在本例中，附認股權證債券內含報酬率比普通債券低1.02%（9%-7.98%）,。
提示仿照教材例題,，本題沒有考慮認股權證行權對股價的稀釋效應影響。也可以理解為5%的股價增長率是市場預測到未來行權可能之后仍能保持5%的增長率,。
在考試時,，看清楚是否需要計算認股權證行權后的股價,，并基于行權后的股權來計算行權凈收入,。
行權后股價=（行權前股價×行權前股份數(shù)+行權價格×認購股份數(shù)）/（行權前股份數(shù)+認購股份數(shù)）
（4）設調整后的票面利率為i，則應有：
1000×i×（P/A,，9%,，20）+206.4×（P/F，9%,，10）+1000×（P/F,，9%，20）-1000=0
求解得：i=8.05%,，（進位取整）i=9%
（5）設調整后的行權價格為X元,，則應有
70×（P/A，9%,，20）+（29.32-X）×20×（P/F,，9%，10）+1000×（P/F，9%,，20）-1000=0
求解得：X=7.7（元）,，（退位取整）X=7元。
備注29.32=18×（1+5%）^10,。
查看完整問題
丁老師
2024-08-19 16:41:36 507人瀏覽
尊敬的學員,，您好：
一般來說，附認股權證債券和可轉債通常都是按年支付利息的,，這是債券市場的一個慣例,。雖然題目中沒有明確說明，但我們可以根據(jù)這個慣例來理解,。當然,，具體的支付頻率（如半年支付一次或按季度支付等）可能會根據(jù)債券的發(fā)行條款有所不同。對于可轉債,，其支付利息的方式通常與普通債券相同,，也是按年支付。同時,，可轉債還賦予持有人在一定期限內將債券轉換為公司股票的權利,，這是其與普通債券的一個主要區(qū)別。
可以打印準考證啦,，記得打印準考證哦~有幫助(1)
答案有問題,？
相關答疑
-
2024-08-16
-
2024-01-08
-
2023-07-03
-
2022-05-11
-
2020-06-01
津公網(wǎng)安備12010202000755號