2015《財務(wù)成本管理》綜合題易考點：投資組合的風(fēng)險和報酬

　　【東奧小編】現(xiàn)階段進入2015年注會強化提高沖刺備考期,，為幫助考生們在最后階段提高備考效率,，我們根據(jù)2015年注冊會計師考試大綱為考生們總結(jié)了《財務(wù)成本管理》科目的選擇題、計算分析題和綜合題易考點,，下面我們一起來復(fù)習(xí)2015《財務(wù)成本管理》綜合題易考點：投資組合的風(fēng)險和報酬,。

　　本考點能力等級：

　　能力等級 3—— 綜合運用能力

　　考生應(yīng)當(dāng)在理解基本理論、基本原理和相關(guān)概念的基礎(chǔ)上,，在比較復(fù)雜的職業(yè)環(huán)境上,，堅守職業(yè)價值觀、遵循職業(yè)道德,、堅持職業(yè)態(tài)度,，綜合運用相關(guān)專業(yè)學(xué)科知識和職業(yè)技能解決實務(wù)問題,。

　　本知識點屬于《財務(wù)成本管理》科目第四章價值評估基礎(chǔ)第二節(jié)風(fēng)險與報酬的內(nèi)容。

　　綜合題易考點：投資組合的風(fēng)險和報酬

　　投資組合理論

　　投資組合理論認(rèn)為,，若干種證券組成的投資組合,，其收益是這些證券收益的加權(quán)平均數(shù)，但是其風(fēng)險不是這些證券風(fēng)險的加權(quán)平均風(fēng)險,，投資組合能降低風(fēng)險,。

　　(一)證券組合的期望報酬率

　　各種證券期望報酬率的加權(quán)平均數(shù)

　　(二)投資組合的風(fēng)險計量

　　基本公式

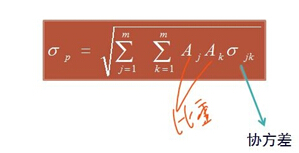
　　1.協(xié)方差的含義與確定

σ_jk=r_jkσ_jσ_k

　　2.相關(guān)系數(shù)的確定

　　3.

　　【提示1】相關(guān)系數(shù)介于區(qū)間[-1,1]內(nèi)。當(dāng)相關(guān)系數(shù)為-1,，表示完全負(fù)相關(guān),，表明兩項資產(chǎn)的收益率變化方向和變化幅度完全相反。當(dāng)相關(guān)系數(shù)為+1時,，表示完全正相關(guān),，表明兩項資產(chǎn)的收益率變化方向和變化幅度完全相同。當(dāng)相關(guān)系數(shù)為0表示不相關(guān),。

　　【提示2】相關(guān)系數(shù)的正負(fù)與協(xié)方差的正負(fù)相同,。相關(guān)系數(shù)為正值，表示兩種資產(chǎn)收益率呈同方向變化,，組合抵消的風(fēng)險較少;負(fù)值則意味著反方向變化,，抵消的風(fēng)險較多。

　　3.兩種證券投資組合的風(fēng)險衡量

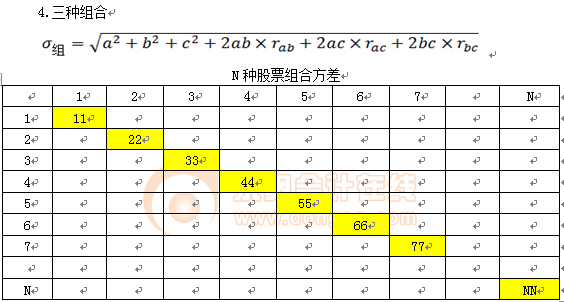
　　【提示】充分投資組合的風(fēng)險,，只受證券之間協(xié)方差的影響，而與各證券本身的方差無關(guān),。

　　5.相關(guān)結(jié)論

　　(1)

　　(2)相關(guān)系數(shù)與組合風(fēng)險之間的關(guān)系

　　(3)

　　6.投資機會集曲線的含義

　　(1)兩種投資組合的投資機會集曲線描述不同投資比例組合的風(fēng)險和報酬的關(guān)系;

　　(2)兩種以上證券的所有可能組合會落在一個平面中。

　　表4-5     不同投資比例的組合

　　(四)有效集

　　理解：有效資產(chǎn)組合曲線是一個由特定投資組合構(gòu)成的集合,。集合內(nèi)的投資組合在既定的風(fēng)險水平上,，期望報酬率是最高的，或者說在既定的期望報酬率下,，風(fēng)險是最低的,。投資者絕不應(yīng)該把所有資金投資于有效資產(chǎn)組合曲線以下的投資組合。

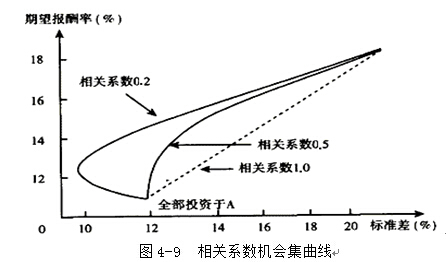
　　(五)相關(guān)系數(shù)與機會集的關(guān)系

　　(六)

　　(六)資本市場線

　　存在無風(fēng)險投資機會時的組合報酬率和風(fēng)險的計算公式

　　總期望報酬率=Q×(風(fēng)險組合的期望報酬率)+(1-Q)×(無風(fēng)險利率)

　　總標(biāo)準(zhǔn)差=Q×風(fēng)險組合的標(biāo)準(zhǔn)差

　　其中：

　　Q代表投資者自有資本總額中投資于風(fēng)險組合的比例，“1-Q”代表投資于無風(fēng)險資產(chǎn)的比例,。

　　【提示】如果貸出資金,，Q將小于1;如果是借入資金，Q會大于1,。

　　(七)風(fēng)險的分類

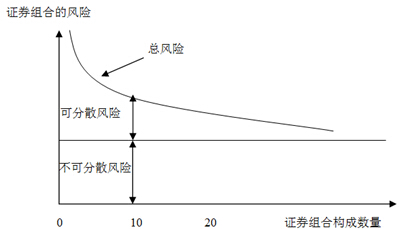
　　【提示1】可以通過增加組合中資產(chǎn)的數(shù)目而最終消除的風(fēng)險被稱為非系統(tǒng)風(fēng)險,，而那些反映資產(chǎn)之間相互關(guān)系,，共同運動,，無法最終消除的風(fēng)險被稱為系統(tǒng)風(fēng)險。

　　【提示2】在風(fēng)險分散過程中,，不應(yīng)當(dāng)過分夸大資產(chǎn)多樣性和資產(chǎn)個數(shù)作用,。一般來講，隨著資產(chǎn)組合中資產(chǎn)個數(shù)的增加,，資產(chǎn)組合的風(fēng)險會逐漸降低,，當(dāng)資產(chǎn)的個數(shù)增加到一定程度時，組合風(fēng)險的降低將非常緩慢直到不再降低,。

　　(八)重點把握的結(jié)論

　　1.證券組合的風(fēng)險不僅與組合中每個證券的報酬率標(biāo)準(zhǔn)差有關(guān),，而且與各證券之間報酬率的協(xié)方差有關(guān)。

　　2.對于一個含有兩種證券的組合,，投資機會集曲線描述了不同投資比例組合的風(fēng)險和報酬之間的權(quán)衡關(guān)系,。

　　3.風(fēng)險分散化效應(yīng)有時使得機會集曲線向左凸出，并產(chǎn)生比最低風(fēng)險證券標(biāo)準(zhǔn)差還低的最小方差組合,。

　　4.有效邊界就是機會集曲線上從最小方差組合點到最高期望報酬率的那段曲線,。

　　5.持有多種彼此不完全正相關(guān)的證券可以降低風(fēng)險。

　　6.如果存在無風(fēng)險證券,，新的有效邊界是經(jīng)過無風(fēng)險利率并和機會集相切的直線,，該直線稱為資本市場線，該切點被稱為市場組合,，其他各點為市場組合與無風(fēng)險投資的有效搭配,。

　　7.資本市場線橫坐標(biāo)是標(biāo)準(zhǔn)差，縱坐標(biāo)是報酬率,。該直線反映兩者的關(guān)系即風(fēng)險價格,。