問題來源：
【2016?計(jì)算分析題（部分）】小Y購買個(gè)人住房向甲銀行借款500,000元,，年報(bào)價(jià)利率8%，每半年計(jì)息一次,，期限5年，自2014年1月1日至2019年1月1日止,，小Y選擇等額本息還款方式償還貸款本息，還款日在每年的7月1日和1月1日,。
要求：
（1）計(jì)算當(dāng)前每期還款額,。
（2）2015年12月末小Y收到單位發(fā)放的一次性年終獎100,000元，如果小Y選擇2016年1月1日提前償還銀行借款100,000元（當(dāng)日仍需償還原定的每期還款額）,，計(jì)算提前還款后的每期還款額。
【答案】（1）計(jì)息期利率=8%/2=4%,，共有10個(gè)計(jì)息期，查年金現(xiàn)值系數(shù)表可得（P/A,，4%,，10）=8.1109
由公式P=A×（P/A,，i，n）,，代入數(shù)據(jù)500,000=A×（P/A，4%,，10）
求得,，當(dāng)前每期還款額A=61,645.44（元）
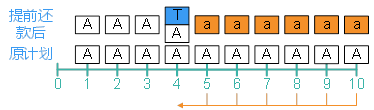
（2）解法一
站在4時(shí)點(diǎn),，未來按照原計(jì)劃還款6次，和提前還款10萬元加按照新計(jì)劃還款6次的現(xiàn)值相等,。
查年金現(xiàn)值系數(shù)表可得（P/A，4%,，6）=5.2421
61,645.44×（P/A，4%,，6）=100,000+a×（P/A，4%,，6）
求得，提前還款后的每期還款額a=42,569.12（元）
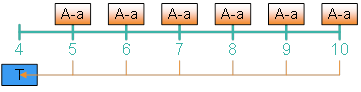
解法二
站在4時(shí)點(diǎn),，由于提前還款10萬元，未來還款金額將從A下降為a,。因此一組等額定期的現(xiàn)金流A-a的現(xiàn)值就是10萬元。
（61,645.44-a）×（P/A,，4%，6）=100,000
求得提前還款后的每期還款額a=42,569.12（元）,。
李老師
2020-09-29 19:36:00 1091人瀏覽
2014年1月1日并沒有支付現(xiàn)金流，是從2014年7月1日開始支付的,，到2019年1月1日支付最后一期，一共是10期,，不是9期,。
2014年7月1日,，2015年1月1日,，2015年7月1日,，2016年1月1日，2016年7月1日,，2017年1月1日,，2017年7月1日,，2018年1月1日，2018年7月1日,，2019年1月1日，一共是10期,。
每天努力,，就會看到不一樣的自己,，加油！相關(guān)答疑
-
2025-01-05
-
2025-01-04
-
2024-11-30
-
2024-11-26
-
2024-08-17
您可能感興趣的CPA試題
津公網(wǎng)安備12010202000755號