證券資產(chǎn)組合的收益與風(fēng)險(xiǎn)_2024年中級(jí)會(huì)計(jì)財(cái)務(wù)管理預(yù)習(xí)知識(shí)點(diǎn)




在備考中級(jí)會(huì)計(jì)師考試的過(guò)程中,。努力了就會(huì)有收獲,下面為大家整理的2024年中級(jí)會(huì)計(jì)考試預(yù)習(xí)階段的知識(shí)點(diǎn),希望對(duì)大家的學(xué)習(xí)有一定的幫助,!

【知識(shí)點(diǎn)】證券資產(chǎn)組合的收益與風(fēng)險(xiǎn)
【所屬章節(jié)】第二章 財(cái)務(wù)管理基礎(chǔ)

證券資產(chǎn)組合的收益與風(fēng)險(xiǎn)
1.資產(chǎn)組合的概念
兩個(gè)或兩個(gè)以上資產(chǎn)所構(gòu)成的集合,,即資產(chǎn)組合,。如果資產(chǎn)組合中的資產(chǎn)均為有價(jià)證券,,則該資產(chǎn)組合也稱為證券資產(chǎn)組合或證券組合,。
2.證券資產(chǎn)組合的預(yù)期收益率
證券資產(chǎn)組合的預(yù)期收益率是組成證券資產(chǎn)組合的各種資產(chǎn)收益率的加權(quán)平均數(shù),,其權(quán)數(shù)為各種資產(chǎn)在組合中的價(jià)值比例,。
3.證券資產(chǎn)組合的風(fēng)險(xiǎn)及其衡量
盡管收益率的方差、標(biāo)準(zhǔn)差,、標(biāo)準(zhǔn)差率是衡量風(fēng)險(xiǎn)的有效工具,,但當(dāng)某項(xiàng)資產(chǎn)或證券成為投資組合的一部分時(shí),這些指標(biāo)就可能不再是衡量風(fēng)險(xiǎn)的有效工具,。
證券資產(chǎn)組合的風(fēng)險(xiǎn)不是各項(xiàng)資產(chǎn)風(fēng)險(xiǎn)簡(jiǎn)單的加權(quán)平均計(jì)算,,要考慮資產(chǎn)收益率之間存在相關(guān)性。證券資產(chǎn)組合的風(fēng)險(xiǎn)會(huì)受到資產(chǎn)之間相關(guān)系數(shù)的影響,。
指標(biāo) | 公式 |
兩種證券投資組合 的標(biāo)準(zhǔn)差(σp) |
W:權(quán)重,,σ:標(biāo)準(zhǔn)差,ρ1,2:證券的相關(guān)系數(shù) |
(1)相關(guān)系數(shù)
相關(guān)系數(shù)是反映兩項(xiàng)資產(chǎn)收益率的相關(guān)程度,,即兩項(xiàng)資產(chǎn)收益率之間的相對(duì)運(yùn)動(dòng)狀態(tài),,用ρ表示。理論上,,相關(guān)系數(shù)介于區(qū)間[-1,,1]內(nèi)。(理解:肉價(jià)上漲——燒烤店or養(yǎng)殖場(chǎng)or服裝店)
(2)風(fēng)險(xiǎn)的分類
絕大多數(shù)資產(chǎn)兩兩之間都具有不完全的相關(guān)關(guān)系,,即相關(guān)系數(shù)小于1且大于-1(多數(shù)情況下大于零),。
因此,大多數(shù)情況下,證券資產(chǎn)組合能夠分散風(fēng)險(xiǎn),,但不能完全消除風(fēng)險(xiǎn),。
根據(jù)風(fēng)險(xiǎn)是否可以被分散,分為可分散風(fēng)險(xiǎn)和不可分散風(fēng)險(xiǎn),。
名稱 | 非系統(tǒng)性風(fēng)險(xiǎn):可分散風(fēng)險(xiǎn),、特有風(fēng)險(xiǎn)、特殊風(fēng)險(xiǎn) | 系統(tǒng)性風(fēng)險(xiǎn):不可分散風(fēng)險(xiǎn),、市場(chǎng)風(fēng)險(xiǎn) |
概念 | 在證券資產(chǎn)組合中,,能夠隨著資產(chǎn)種類增加而降低直至消除的風(fēng)險(xiǎn),即發(fā)生于個(gè)別公司特有事件造成的風(fēng)險(xiǎn) | 影響所有資產(chǎn)的,、不能通過(guò)資產(chǎn)組合消除的風(fēng)險(xiǎn),,也就是不能隨著資產(chǎn)種類增加而分散的風(fēng)險(xiǎn) |
舉例 | 員工罷工、新產(chǎn)品開(kāi)發(fā)失敗,、失去重要的銷售合同,、訴訟失敗,或者宣告發(fā)現(xiàn)新礦藏,、取得一個(gè)重要合同等 | 國(guó)家政策變化,、稅制改革、企業(yè)會(huì)計(jì)準(zhǔn)則改革,、世界能源狀況,、政治因素等 |
(3)貝塔系數(shù)(β系數(shù))
不同資產(chǎn)的系統(tǒng)性風(fēng)險(xiǎn)不同,所以用β系數(shù)衡量資產(chǎn)的系統(tǒng)性風(fēng)險(xiǎn)的大小,。它告訴我們相對(duì)于市場(chǎng)組合而言特定資產(chǎn)的系統(tǒng)性風(fēng)險(xiǎn)是多少,。
市場(chǎng)組合 | 是由市場(chǎng)上所有資產(chǎn)組成的組合,其非系統(tǒng)性風(fēng)險(xiǎn)已經(jīng)被消除,,所以市場(chǎng)組合的風(fēng)險(xiǎn)就是市場(chǎng)風(fēng)險(xiǎn)或系統(tǒng)性風(fēng)險(xiǎn),,市場(chǎng)組合相對(duì)于它自己的β系數(shù)是1 【提示】市場(chǎng)組合的收益率是市場(chǎng)的平均收益率,用Rm表示 |
某資產(chǎn)的 β系數(shù) | 表示該資產(chǎn)的系統(tǒng)性風(fēng)險(xiǎn)相當(dāng)于市場(chǎng)組合系統(tǒng)性風(fēng)險(xiǎn)的倍數(shù),,即相對(duì)于市場(chǎng)組合而言特定資產(chǎn)的系統(tǒng)性風(fēng)險(xiǎn)是多少 |
不同大小β系數(shù)的含義:
β系數(shù)大小 | 含義 | 波動(dòng)幅度 | |
β>0 | β>1 | 其收益率的變化與市場(chǎng)收益率變化同向 | >市場(chǎng)組合波動(dòng) |
β=1 | =市場(chǎng)組合波動(dòng) | ||
0<β<1 | <市場(chǎng)組合波動(dòng) | ||
β<0 | 極個(gè)別資產(chǎn)的β系數(shù)為負(fù)數(shù),,即該資產(chǎn)收益率與市場(chǎng)收益率變化反向,如西方個(gè)別收賬公司和個(gè)別再保險(xiǎn)公司的β系數(shù)是接近于零的負(fù)數(shù) | ||
注:以上中級(jí)會(huì)計(jì)考試學(xué)習(xí)內(nèi)容選自楊樹(shù)林老師2023年《財(cái)務(wù)管理》授課講義
(本文為東奧會(huì)計(jì)在線原創(chuàng)文章,,僅供考生學(xué)習(xí)使用,,禁止任何形式的轉(zhuǎn)載)
精選推薦
報(bào)考咨詢中心 資深財(cái)會(huì)老師為考生解決報(bào)名備考相關(guān)問(wèn)題 立即提問(wèn)






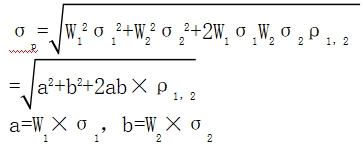

































 津公網(wǎng)安備12010202000755號(hào)
津公網(wǎng)安備12010202000755號(hào)