兩項資產(chǎn)組合的風險與收益_2020年中級會計財務管理預習知識點
一分耕耘一分收獲，努力越大，收獲越多。中級會計預習備考階段已經(jīng)開始，大家現(xiàn)在開始就要將基礎(chǔ)打好,，小編期待大家順利通過的好消息！
【內(nèi)容導航】
兩項資產(chǎn)組合的風險與收益
【所屬章節(jié)】
第二章 財務管理基礎(chǔ)
【知識點】兩項資產(chǎn)組合的風險與收益
兩項資產(chǎn)組合的風險與收益
兩個或兩個以上資產(chǎn)所構(gòu)成的集合,，稱為資產(chǎn)組合,。如果資產(chǎn)組合中的資產(chǎn)均為有價證券，則該資產(chǎn)組合也可稱為證券組合,。
組合方式 及相關(guān)概念 | 投資組合的期望收益率 | 投資組合的風險 |
兩種 證券 | E（ 不論投資組合中兩只證券之間的相關(guān)系數(shù)如何,，只要投資比例不變,，各只證券的期望收益率不變，則該投資組合的期望收益率就不變,，即投資組合的期望收益率與其相關(guān)系數(shù)無關(guān) |
在其他條件不變時,，如果兩只股票收益率的相關(guān)系數(shù)越小，組合的方差就越小,，表明組合后的風險越低,，組合中分散掉的風險越大，其投資組合可分散的風險的效果就越大,。即投資組合的風險與其相關(guān)系數(shù)正相關(guān) |
相關(guān) 系數(shù) | 相關(guān)系數(shù)反映兩項資產(chǎn)收益率的相關(guān)程度,，即兩項資產(chǎn)收益率之間的相對運動狀態(tài)。 相關(guān)系數(shù)總是在-1到+1之間的范圍內(nèi)變動,，-1代表完全負相關(guān),，1代表完全正相關(guān)，0則表示不相關(guān) | |
兩種證券 組合的 討論 | 投資組合的方差 （1）當 投資組合的標準差為單項資產(chǎn)標準差的加權(quán)平均數(shù)，即當兩項資產(chǎn)的收益率完全正相關(guān)時,，兩項資產(chǎn)的風險完全不能互相抵消,，所以這樣的資產(chǎn)組合不能降低任何風險。 （2）當 即當兩項資產(chǎn)的收益率完全負相關(guān)時,，兩者之間的風險可以充分地相互抵消,，甚至完全消除（但限于非系統(tǒng)性風險）。 （3）當 | |
總結(jié) | 在證券資產(chǎn)組合中，能夠隨著資產(chǎn)種類增加而降低直至消除的風險,，被稱為非系統(tǒng)性風險,；不能隨著資產(chǎn)種類增加而分散的風險,，被稱為系統(tǒng)性風險 | |
注：以上中級會計考試預習階段知識點選自田明老師《財務管理》授課講義
(本文為東奧會計在線原創(chuàng)文章，僅供考生學習使用,，禁止任何形式的轉(zhuǎn)載)
相關(guān)文章
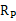
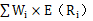
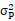
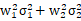
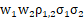
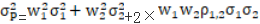
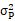
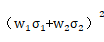
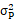
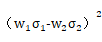
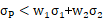
津公網(wǎng)安備12010202000755號