CPA財管考前重點學習筆記——資本市場線與證券市場線
距離2021年注冊會計師考試僅剩兩個月,,《財管》科目大家復習準備的怎么樣呢?為了幫助大家順利備考,,東奧特整理了CPA財管考前重點學習筆記,,快來和小編一起打開學習吧!更多CPA財管考前重點學習筆記戳我查看>>>
【重要知識點】
統(tǒng)計公式:
| ||||
機會集:隨著對兩種證券投資比例的改變,,投資組合風險和報酬之間的權(quán)衡關(guān)系 | ||||
風險
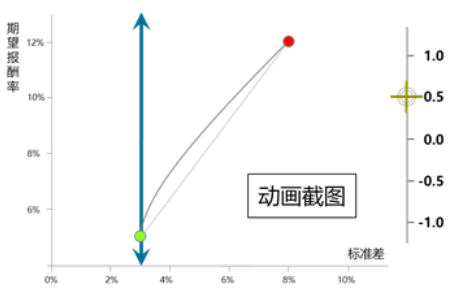
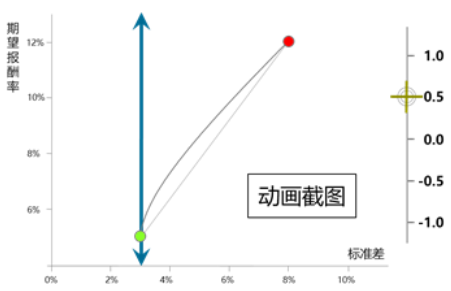
| 兩項資產(chǎn)組合的標準差(代表總體風險)= 不能直接加權(quán)平均計算 當兩者完全正相關(guān)r12=1時,,組合標準差等于各項資產(chǎn)標準差的加權(quán)平均; 當兩者不完全正相關(guān)r12<1時,,組合標準差小于各項資產(chǎn)標準差的加權(quán)平均(風險分散效應(yīng)) 這里可以直接代入公式,,也可以單純靠理解,像買股票一樣,,完全正相關(guān)說明兩支股票它漲它也漲,,它跌它也跟著跌,這樣沒法降低風險,;不完全正相關(guān)時,,一支跌了,另一支有可能在漲,,你就有可能不賠,,可以適當降低風險,。 | 綠點為低風險低收益資產(chǎn),紅點為高風險高收益資產(chǎn),。 相關(guān)系數(shù)r不夠小時
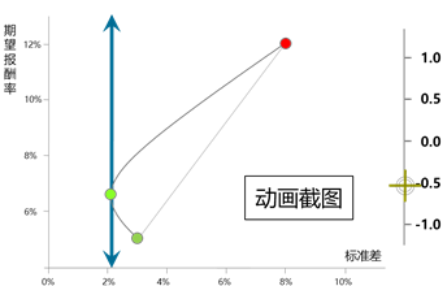
相關(guān)系數(shù)r足夠小時
| ||
收益 | 兩項資產(chǎn)組合的期望報酬率(代表收益) 可以直接加權(quán)平均計算 組合期望報酬率等于各項資產(chǎn)期望報酬率的加權(quán)平均 | |||
圖像是否變動 | 各資產(chǎn)投資比例變化時→點在機會集曲線上移動 相關(guān)系數(shù)r變小時→機會集曲線向左凸,,向左凸的程度越大,風險分散效應(yīng)越大 | |||
圖像解讀 | ||||
當相關(guān)系數(shù)不夠小時(機會集曲線沒有突破低風險資產(chǎn)的左側(cè)) | 當相關(guān)系數(shù)足夠小時(機會集曲線突破了低風險資產(chǎn)的左側(cè)) | |||
有效邊界 | 有效邊界=機會集曲線 無效集為空 | 有效邊界<機會集曲線(為最小方差組合以上的部分) 無效集為最小方差組合以下的部分 | ||
最高收益 | 圖像上界=最高收益=高風險資產(chǎn)收益 | 圖像上界=最高收益=高風險資產(chǎn)收益 | ||
最低收益 | 圖像下界=最低收益=低風險資產(chǎn)收益 | 圖像下界=最低收益=低風險資產(chǎn)收益 | ||
最高風險 | 圖像右界=最高風險=高風險資產(chǎn)風險 | 圖像右界=最高風險=高風險資產(chǎn)風險 | ||
最低風險 | 圖像左界=最低風險=低風險資產(chǎn)風險 | 圖像左界=最低風險<低風險資產(chǎn)風險 | ||
最小方差組合 | 最小方差組合與低風險點重合 | 最小方差組合移動到低風險點的左側(cè) | ||
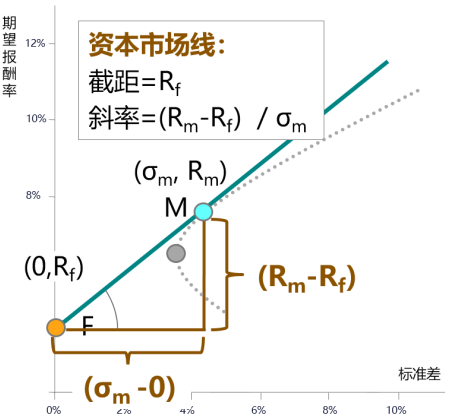
資本市場線:體現(xiàn)了持有不同比例的無風險資產(chǎn)和市場組合情況下風險和期望報酬率的權(quán)衡關(guān)系 | ||||
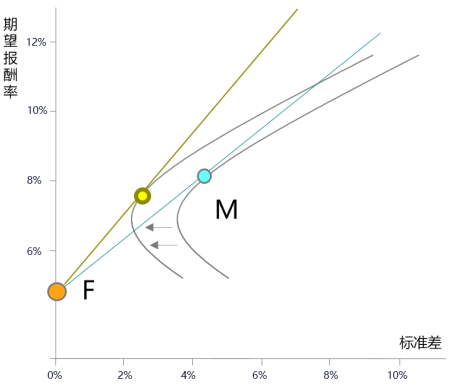
市場均衡點特征: (1)資本市場線與有效邊界的切點 (2)所有證券以各自市值為權(quán)重的組合 (3)唯一有效的最佳風險資產(chǎn)組合(引入無風險資產(chǎn)后,,除市場均衡點外,,其余機會集上的有效點均不再有效) (4)所有投資者共同決定的,不受單個投資者影響 | Ri=Rf+(Rm-Rf)/σm×σi
F點為無風險收益率點,,M點為市場均衡點(機會集與資本市場線的切點,,當資本市場線上的點處于M點上方時,表明投資者借入無風險資金來進行投資) | |||
風險 | σi=Q×σm 資產(chǎn)組合標準差的加權(quán)平均 | |||
收益 | Ri=Q×Rm+(1-Q)×Rf
| |||
圖像變化 | 下圖為幾種因素改變后,,對資本市場線的影響: 可以從資本市場線公式Ri=Rf+(Rm-Rf)/σm×σi來判斷,,截距為Rf,,斜率為(Rm-Rf)/σm,風險資產(chǎn)的收益影響(Rm-Rf),風險資產(chǎn)的標準差影響σm | |||
| 風險資產(chǎn)收益和標準差不變,無風險利率升高→整體資本市場線上移,截距增加,斜率不變
| |||
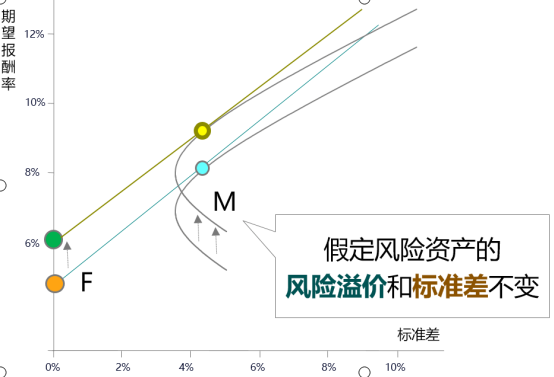
| 無風險利率,、風險資產(chǎn)標準差不變,,風險資產(chǎn)收益增加→資本市場線截距不變,,斜率增加 | |||
| 無風險利率、風險資產(chǎn)收益不變,,風險資產(chǎn)標準差減小→資本市場線截距不變,,斜率增加 | |||
| 無風險利率、風險資產(chǎn)收益,、標準差均不變,,投資者改變投資比例→資本市場線本身不發(fā)生變化,,僅是線上點的移動 | |||
證券市場線: 市場均衡條件下任何資產(chǎn)或組合的風險和必要報酬率之間的權(quán)衡關(guān)系 CAPM公式:Ri=Rf+(Rm-Rf)×βi | ||||
X軸:風險 | 用β表示,代表資產(chǎn)系統(tǒng)風險對市場組合風險的相對值(取值范圍),,市場組合系統(tǒng)風險為1,,β的四種計算方法: ①定義式:
②關(guān)系式: (與股票市場間相關(guān)系數(shù)、股票自身標準差同向變動,,整個市場標準差反向變動) ③回歸直線法: ④已知Ri使用CAPM公式反推βi:βi=(Ri-Rf)/(Rm-Rf)=個股風險溢價/市場風險溢價 投資組合的β系數(shù)可以加權(quán)平均,,可以度量特定資產(chǎn)對整體組合風險的貢獻 | |||
Y軸:收益 | 必要報酬率 | |||
圖像變化 | 預計通貨膨脹率上升,市場風險溢價保持不變→證券市場線截距增加,,系數(shù)不變 | |||
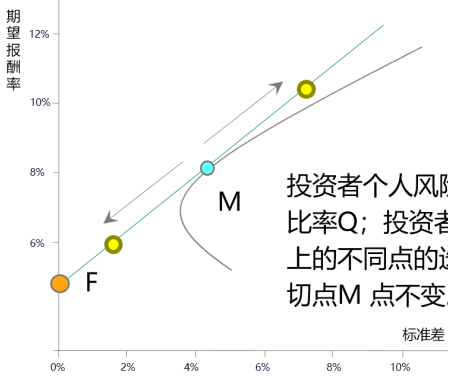
投資者風險厭惡情緒提高,,無風險利率保持不變→證券市場線截距不變,系數(shù)增加(投資者更厭惡風險就需要更高的風險溢價) | ||||
某項投資系統(tǒng)風險增加,,無風險利率和市場風險溢價不變→證券市場線不變,,線上從一個點滑到另一個點 | ||||
● 機會集、資本線與證券線對比
機會集 | 資本線 | 證券線 | |
公式 | — | Ri=Rf+(Rm-Rf)/σm×σi | Ri=Rf+(Rm-Rf)×βi |
定義 | 持有不同投資比例(風險資產(chǎn))組合的風險和報酬之間的權(quán)衡關(guān)系 | 持有不同比例無風險資產(chǎn)和市場組合情況下風險和期望報酬率之間的權(quán)衡關(guān)系 | 市場均衡條件下任何資產(chǎn)或組合的風險和必要報酬率的權(quán)衡關(guān)系 |
收益(Y軸) | 預期報酬率 (各資產(chǎn)各自預期報酬率的加權(quán)平均) | 預期報酬率 無風險資產(chǎn)利率與市場組合資產(chǎn)預期報酬率的加權(quán)平均
| 必要收益率 多項資產(chǎn)組合的必要收益率等于各資產(chǎn)必要收益率的加權(quán)平均 |
風險(X軸) | 標準差(衡量總風險,、當資產(chǎn)間不完全正相關(guān)時,,不可加權(quán)計算) | 標準差(衡量總風險)
| β系數(shù),衡量系統(tǒng)風險(可加權(quán)計算) |
點沿著線滑動 | 投資比例的變化(W1W2) | 個人風險偏好變化 (無風險資產(chǎn)與市場組合資產(chǎn)組合比例) | 系統(tǒng)風險變化 |
線的移動 | 相關(guān)系數(shù)(r)變化 | 無風險利率、風險組合期望報酬率,、標準差的變化 | 無風險利率,、市場風險溢價的變化 |
【答題筆記】
證券市場線用β來表示風險,β表示資產(chǎn)的系統(tǒng)風險相對于市場組合的比例,,市場組合的系統(tǒng)風險為1,。當β大于1的時候,表示資產(chǎn)的系統(tǒng)風險大于市場組合整體的風險,;等于1的時候,,表示資產(chǎn)的系統(tǒng)風險等于市場組合整體的風險,當其小于0的時候,,表示資產(chǎn)收益與市場平均收益反方向變動,。
以上就是東奧小編為大家整理的關(guān)于資本市場線與證券市場線的相關(guān)內(nèi)容,考生們要認真學習哦,!注會考試時間為8月27日-29日,,考生們要充分利用剩余的時間進行備考,爭取順利通過考試,!
(本文為東奧會計在線原創(chuàng)文章,,僅供考生學習使用,禁止任何形式的轉(zhuǎn)載)
注冊會計師導航
-
考試資訊
-
考試資料
考試資料 | 會計 | 審計 | 稅法 | 經(jīng)濟法 | 財管 | 戰(zhàn)略 | 考試經(jīng)驗 | 考試大綱 | 免費答疑
-
輔導課程
-
考試題庫
-
互動交流
-
東奧書店






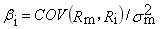
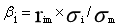










































 津公網(wǎng)安備12010202000755號
津公網(wǎng)安備12010202000755號