最優(yōu)存貨量的確定_2022年中級會計財務(wù)管理每日鞏固一考點

來源：東奧會計在線責編：祝艷2022-08-22 15:06:57

比別人多一點耐心、多一點毅力,，或許夢想就在不遠處等你,。今日份中級會計《財務(wù)管理》相關(guān)知識點已更新，快來跟著東奧會計在線一起來學習吧,！

【知識點】最優(yōu)存貨量的確定(也叫做經(jīng)濟訂貨批量)

(一)經(jīng)濟訂貨基本模型

假設(shè)	（1）存貨總需求量是已知常數(shù),；（2）不存在訂貨提前期，即可以隨時補充存貨,；（3）貨物是一次性入庫,；（4）單位貨物成本為常數(shù),，無批量折扣；（5）庫存儲存成本與庫存水平呈線性關(guān)系,；（6）貨物是一種獨立需求的物品,，不受其他貨物影響；（7）不允許缺貨,，即無缺貨成本,，TCs為零
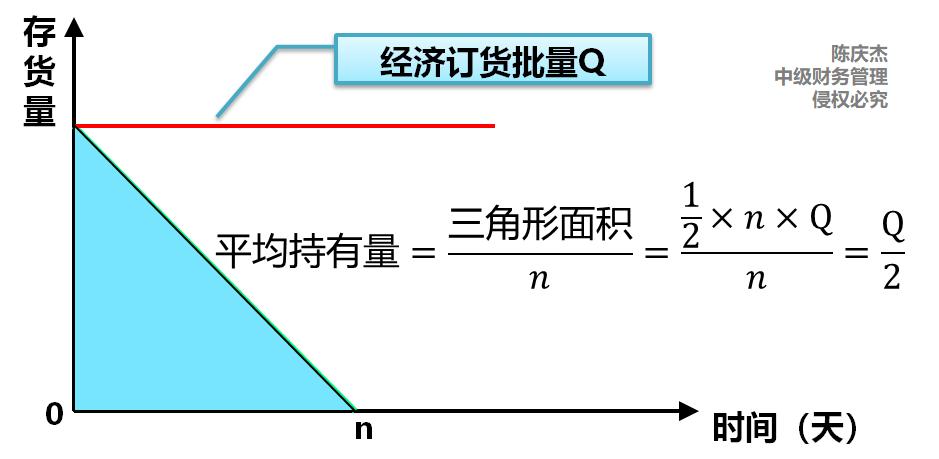
相關(guān) 成本	（1）儲存變動成本	Q/2×KC
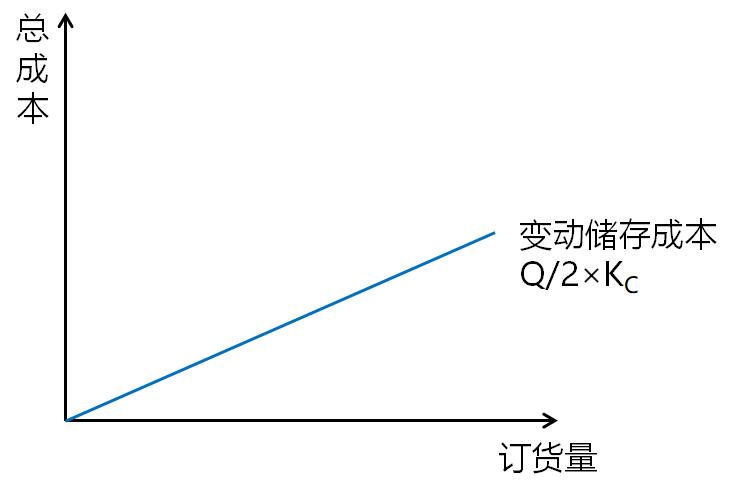
	（2）訂貨變動成本	D/Q×K
	總成本	總成本=Q/2×KC＋D/Q×K
計算

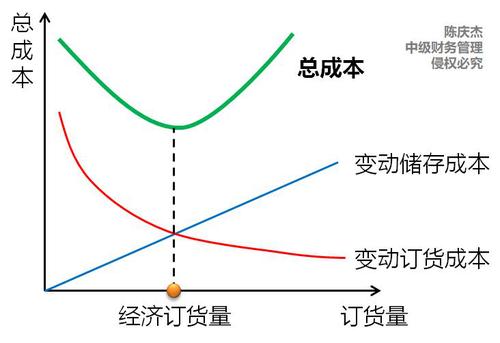
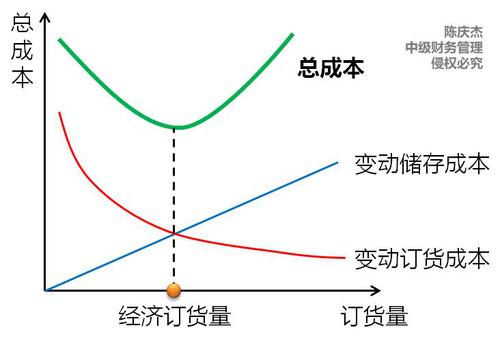
結(jié)論

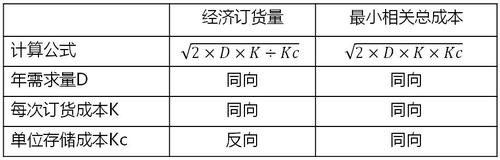
【對比】

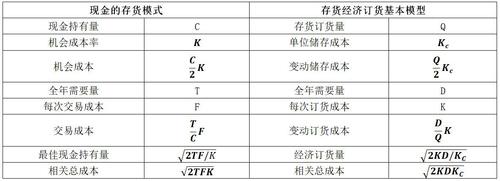
(二)經(jīng)濟訂貨基本模型的擴展

放寬經(jīng)濟訂貨基本模型的相關(guān)假設(shè)，就可以擴展經(jīng)濟訂貨模型,，以擴大其適用范圍,。

1.再訂貨點

模型假設(shè)	（1）交貨期不為零（放寬基本模型的第二個假設(shè)。雖不能“立即取得存貨”,，但到貨是一次性的）（2）沒有保險儲備
計算公式	企業(yè)再次發(fā)出訂貨單時應(yīng)保持的存貨庫存量＝平均交貨時間×平均每日需求量再訂貨點R=平均交貨時間L×每日平均需用量d
注意	再訂貨點R的單位是產(chǎn)品件數(shù)
經(jīng)濟訂貨量	訂貨提前期對經(jīng)濟訂貨量無影響（每次訂貨批量,、訂貨次數(shù)、訂貨間隔時間等與瞬時補充相同）
特點	企業(yè)在再訂貨點R明確的是,，當存貨還剩多少時就應(yīng)當發(fā)出訂單了只是改變訂貨時間,，沒有改變經(jīng)濟訂貨量，也沒改變批量相關(guān)成本
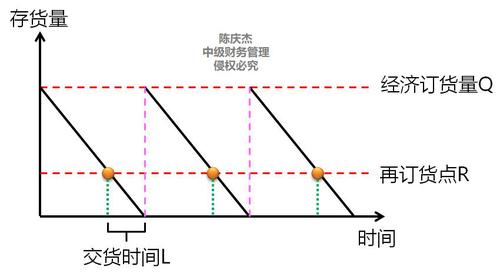
圖示

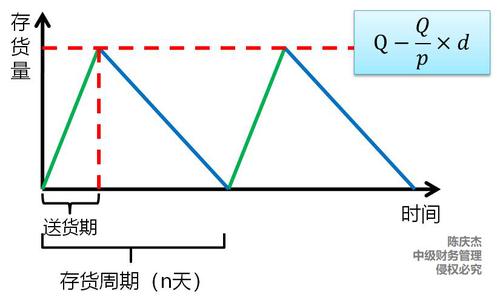
2.存貨陸續(xù)供應(yīng)和使用模型

模型假設(shè)	陸續(xù)到貨（放寬基本模型的第三個假設(shè)“貨物是一次性入庫”,，其他條件不變）
圖示
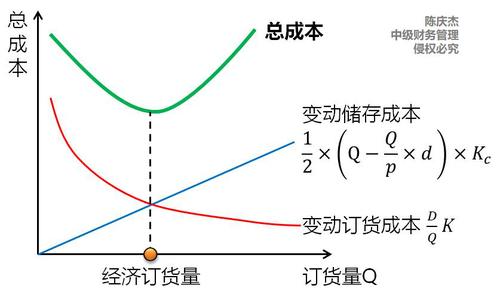
相關(guān)成本	變動存儲成本	Q	每批訂貨數(shù)
		P	每天送貨量
		Q/P	送貨期
		Q/P×d	送貨期內(nèi)的生產(chǎn)耗用量
		Q-Q/P×d	最高庫存量（貨到齊時）
		（Q-Q/P×d）×1/2	平均庫存量
		Kc×（Q-Q/P×d）×1/2	變動存儲成本
	變動訂貨成本	D/Q×K	變動訂貨成本
決策結(jié)果
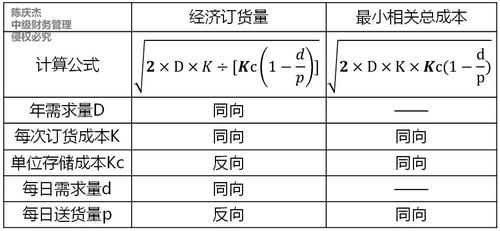
影響因素	【備注】d受D的影響,，如果每年經(jīng)營天數(shù)不變的話，對D與d對最小相關(guān)總成本的影響不確定

(三)保險儲備

原因	1.交貨時間L可能延長 2.日需求量d可能增加
目標	設(shè)立保險儲備,，有保險儲備成本,；不設(shè)保險儲備，可能會有缺貨損失,，找到最佳保險儲備量,，這是使保險儲備量上的儲存成本與缺貨損失之和最低的保險儲備量
假設(shè)	允許缺貨（放寬基本模型的第七個假設(shè)：不允許缺貨）
指標重構(gòu)	再訂貨點=交貨時間×平均日需求＋保險儲備
相關(guān)成本	缺貨損失Cs=Ku×S×N Ku:每個訂貨周期每件產(chǎn)品缺貨損失 S:平均缺貨數(shù)量（缺貨數(shù)量×缺貨概率） N:每年訂貨次數(shù)	存儲成本CB=B×Kc B:保險儲備量（不需要乘1/2） Kc:單位存儲成本【思考】B為什么不需要乘1/2
	相關(guān)總成本=TC（S、B）=KU×S×N＋B×KC
提示	教材只有交貨期內(nèi)需求增加的保險儲備的決策例題,。對于因延誤供貨引起的缺貨,，教材提及一句話：可以通過估計延誤時間和平均每日耗用量來計算增加的保險儲備量，教材沒有例題