2014《財(cái)務(wù)成本管理》預(yù)習(xí)知識(shí)點(diǎn)：布萊克－斯科爾斯期權(quán)定價(jià)模型

　　【小編導(dǎo)言】我們一起來(lái)學(xué)習(xí)2014《財(cái)務(wù)成本管理》預(yù)習(xí)知識(shí)點(diǎn)：布萊克－斯科爾斯期權(quán)定價(jià)模型,。

　　【內(nèi)容導(dǎo)航】：

　　(一)假設(shè)

　　(二)公式

　　(三)參數(shù)估計(jì)

　　(四)看漲期權(quán)—看跌期權(quán)平價(jià)定理

　　(五)派發(fā)股利的期權(quán)定價(jià)

　　(六)美式期權(quán)估價(jià)

　　本知識(shí)點(diǎn)屬于《財(cái)務(wù)成本管理》科目第九章期權(quán)估價(jià)第二節(jié)期權(quán)價(jià)值評(píng)估的方法的內(nèi)容。

　　【知識(shí)點(diǎn)】：布萊克－斯科爾斯期權(quán)定價(jià)模型

　　(一)假設(shè)

　　1.在期權(quán)壽命期內(nèi),，買方期權(quán)標(biāo)的股票不發(fā)放股利,，也不做其他分配;

　　2.股票或期權(quán)的買賣沒(méi)有交易成本;

　　3.短期的無(wú)風(fēng)險(xiǎn)利率是已知的，并且在期權(quán)壽命期內(nèi)保持不變;

　　4.任何證券購(gòu)買者能以短期的無(wú)風(fēng)險(xiǎn)利率借得任何數(shù)量的資金;

　　5.允許賣空,，賣空者將立即得到所賣空股票當(dāng)天價(jià)格的資金;

　　6.看漲期權(quán)只能在到期日?qǐng)?zhí)行;

　　7.所有證券交易都是連續(xù)發(fā)生的,，股票價(jià)格隨機(jī)游走,。

　　(二)公式

　　(三)參數(shù)估計(jì)

　　1.無(wú)風(fēng)險(xiǎn)利率

　　無(wú)風(fēng)險(xiǎn)利率應(yīng)選擇與期權(quán)到期日相同的國(guó)庫(kù)券利率。如果沒(méi)有相同時(shí)間的,，應(yīng)選擇時(shí)間最接近的國(guó)庫(kù)券利率,。

　　這里所說(shuō)的國(guó)庫(kù)券利率是指其市場(chǎng)利率，而不是票面利率,。

　　模型中的無(wú)風(fēng)險(xiǎn)利率是按連續(xù)復(fù)利計(jì)算的利率,。

　　如果用F表示終值，P表示現(xiàn)值,，rc表示無(wú)風(fēng)險(xiǎn)利率,，t表示時(shí)間(年)：

　　則：F=P×e^rct

　　即：rc=[ln(F/P)]/t

　　(四)看漲期權(quán)—看跌期權(quán)平價(jià)定理

　　對(duì)于歐式期權(quán)，假定看漲期權(quán)和看跌期權(quán)有相同的執(zhí)行價(jià)格和到期日,，則下述等式成立：

　　看漲期權(quán)價(jià)格-看跌期權(quán)價(jià)格=標(biāo)的資產(chǎn)的價(jià)格-執(zhí)行價(jià)格的現(xiàn)值

　　這種關(guān)系,，被稱為看漲期權(quán)-看跌期權(quán)平價(jià)定理，利用該等式中的4個(gè)數(shù)據(jù)中的3個(gè),，就可以求出另外1個(gè),。

　　(五)派發(fā)股利的期權(quán)定價(jià)

　　考慮派發(fā)股利的期權(quán)定價(jià)公式如下：

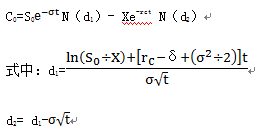
　　在期權(quán)估價(jià)時(shí)要從股價(jià)中扣除期權(quán)到期日前所派發(fā)的全部股利的現(xiàn)值。

　　δ：標(biāo)的股票年股利收益率

　　(六)美式期權(quán)估價(jià)

　　(1)美式期權(quán)在到期前的任意時(shí)間都可以執(zhí)行,，除享有歐式期權(quán)的全部權(quán)力之外,，還有提前執(zhí)行的優(yōu)勢(shì)。因此,，美式期權(quán)的價(jià)值應(yīng)當(dāng)至少等于相應(yīng)歐式期權(quán)的價(jià)值,，在某種情況下比歐式期權(quán)的價(jià)值更大。

　　(2)對(duì)于不派發(fā)股利的美式看漲期權(quán),，可以直接使用布萊克-斯科爾斯模型進(jìn)行估價(jià),。

　　(3)理論上不適合派發(fā)股利的美式期權(quán)股價(jià)。

　　但是BS模型有參考價(jià)值,，誤差不大,。