2017《財務(wù)與會計》基礎(chǔ)考點：證券的估價模型
3.決策原則
當(dāng)股票價值高于股票市價(購買價格),，可以購買。
【例題·單選題】現(xiàn)有兩只股票,，A股票的市價為15元,，B股票的市價為7元，某投資人經(jīng)過測算得出A股票的價值為12元,，B股票的價值為8元,，則下列表達(dá)正確的有( )。
A.股票A比股票B值得投資
B.股票B和股票A均不值得投資
C.應(yīng)投資A股票
D.應(yīng)投資B股票
【答案】D
【解析】A股票價值低于股票市價,，不值得投資,。B股票價值高于股票市價，值得投資,。
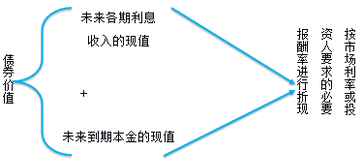
(二)債券估價模型——債券價值的確定
1.債券價值含義(債券本身的內(nèi)在價值)
未來的現(xiàn)金流入的現(xiàn)值
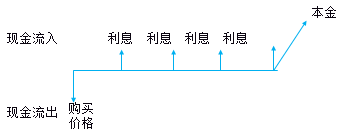
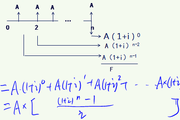
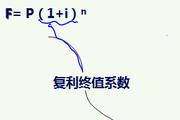
2.計算
(1)分期等額付息的債券估價模型
【教材例題5-16】某公司投資購入一種債券,，該債券的面值為1000元，票面利率為8%,，每年年末付息一次,，期限為10年。若市場利率為10%，則該債券的價值為多少?若市場利率為6%,，則該債券的價值又為多少?
【答案】
根據(jù)債券估價模型,，該債券的價值為：
(1)當(dāng)市場利率為10%時：
P=I×(P/A，k,，n)+A×(P/F,，k，n)
=1000×8%×(P/A,，10%，10)+1000×(P/F,，10%,，10)
=80×6.1446+1000×0.3855=877.1(元)
(2)當(dāng)市場利率為6%時：
P=I×(P/A，k,，n)+A×(P/F,，k,，n)
=1000×8%×(P/A，6%,，10)+1000×(P/F,，6%，10)
=80×7.3601+1000×0.5584=1147.2(元)
【結(jié)論】市場利率與債券價值反向變動,。
(1)當(dāng)市場利率高于票面利率時，債券價值低于債券票面價格;
(2)當(dāng)市場利率低于票面利率時,，債券價值高于債券票面價格;
(3)當(dāng)市場利率等于票面利率時,，債券價值等于債券票面價格。
【提示】
若年內(nèi)付息多次,，年數(shù)變期數(shù),，年利率變期利率,。
相關(guān)文章
津公網(wǎng)安備12010202000755號